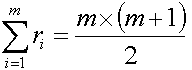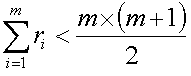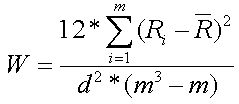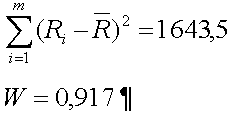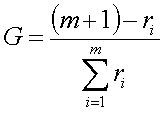–ò—Å–ø–æ–ª—å–∑–æ–≤–∞–Ω–∏–µ –º–µ—Ç–æ–¥–æ–≤ —ç–∫—Å–ø–µ—Ä—Ç–Ω—ã—Ö –æ—Ü–µ–Ω–æ–∫ –≤ –æ—Ü–µ–Ω–æ—á–Ω–æ–π –ø—Ä–∞–∫—Ç–∏–∫–µ
–í –æ—Ü–µ–Ω–æ—á–Ω–æ–π –ø—Ä–∞–∫—Ç–∏–∫–µ –¥–æ—Å—Ç–∞—Ç–æ—á–Ω–æ —á–∞—Å—Ç–æ –∏—Å–ø–æ–ª—å–∑—É—é—Ç—Å—è —ç–∫—Å–ø–µ—Ä—Ç–Ω—ã–µ –æ—Ü–µ–Ω–∫–∏. –í–æ –º–Ω–æ–≥–∏—Ö —Å–ª—É—á–∞—è—Ö —ç—Ç–æ –≤—ã–∑–≤–∞–Ω–æ –æ—Ç—Å—É—Ç—Å—Ç–≤–∏–µ–º –Ω–µ–æ–±—Ö–æ–¥–∏–º–æ–π –∏–Ω—Ñ–æ—Ä–º–∞—Ü–∏–∏. –í —á–∞—Å—Ç–Ω–æ—Å—Ç–∏ –¥–æ—Å—Ç–∞—Ç–æ—á–Ω–æ —Ä–∞—Å–ø—Ä–æ—Å—Ç—Ä–∞–Ω–µ–Ω–æ –∏—Å–ø–æ–ª—å–∑–æ–≤–∞–Ω–∏–µ –º–µ—Ç–æ–¥–∞ —ç–∫—Å–ø–µ—Ä—Ç–Ω—ã—Ö –æ—Ü–µ–Ω–æ–∫ –ø—Ä–∏ –æ–ø—Ä–µ–¥–µ–ª–µ–Ω–∏–∏ –≤–µ—Å–æ–≤ —Ü–µ–Ω–æ–æ–±—Ä–∞–∑—É—é—â–∏—Ö —Ñ–∞–∫—Ç–æ—Ä–æ–≤ –≤ —Ä–∞–∑–ª–∏—á–Ω—ã—Ö –º–µ—Ç–æ–¥–∞—Ö, –∏—Å–ø–æ–ª—å–∑—É–µ–º—ã—Ö –≤ —Å—Ä–∞–≤–Ω–∏—Ç–µ–ª—å–Ω–æ–º –ø–æ–¥—Ö–æ–¥–µ –ø—Ä–∏ –∫–æ—Ä—Ä–µ–∫—Ç–∏—Ä–æ–≤–∫–µ —Ü–µ–Ω –∞–Ω–∞–ª–æ–≥–æ–≤. –û–¥–Ω–∞–∫–æ, –∑–∞—á–∞—Å—Ç—É—é –ø–æ–ª—É—á–µ–Ω–Ω—ã–µ –æ—Ç —ç–∫—Å–ø–µ—Ä—Ç–æ–≤ –æ—Ü–µ–Ω–∫–∏ –∏—Å–ø–æ–ª—å–∑—É—é—Ç—Å—è –±–µ–∑ –ø—Ä–æ–≤–µ—Ä–∫–∏ –Ω–∞ –∏—Ö –ø—Ä–∏–µ–º–ª–µ–º–æ—Å—Ç—å. –í –¥–∞–Ω–Ω–æ–π —Å—Ç–∞—Ç—å–µ –º—ã —Ä–∞—Å—Å–º–æ—Ç—Ä–∏–º –æ–¥–∏–Ω –∏–∑ –º–µ—Ç–æ–¥–æ–≤ –∫–æ–ª–ª–µ–∫—Ç–∏–≤–Ω—ã—Ö —ç–∫—Å–ø–µ—Ä—Ç–Ω—ã—Ö –æ—Ü–µ–Ω–æ–∫ –∏ —Å–ø–æ—Å–æ–± –∞–Ω–∞–ª–∏–∑–∞ –ø–æ–ª—É—á–µ–Ω–Ω—ã—Ö –æ—Ç —ç–∫—Å–ø–µ—Ä—Ç–æ–≤ —Ä–µ–∑—É–ª—å—Ç–∞—Ç–æ–≤ –Ω–∞ –∏—Ö –ø—Ä–∏–µ–º–ª–µ–º–æ—Å—Ç—å –¥–ª—è –¥–∞–ª—å–Ω–µ–π—à–∏—Ö —Ä–∞—Å—á–µ—Ç–æ–≤. –û–¥–Ω–∏–º –∏–∑ —Ä–∞—Å–ø—Ä–æ—Å—Ç—Ä–∞–Ω–µ–Ω–Ω—ã—Ö –∫–æ–ª–ª–µ–∫—Ç–∏–≤–Ω—ã—Ö –º–µ—Ç–æ–¥–æ–≤ —ç–∫—Å–ø–µ—Ä—Ç–Ω—ã—Ö –æ—Ü–µ–Ω–æ–∫ —è–≤–ª—è–µ—Ç—Å—è —Ä–∞–Ω–∂–∏—Ä–æ–≤–∞–Ω–∏–µ. –°—É—Ç—å –ø—Ä–æ—Ü–µ–¥—É—Ä—ã –∑–∞–∫–ª—é—á–∞–µ—Ç—Å—è –≤ —Å–ª–µ–¥—É—é—â–µ–º:—ç–∫—Å–ø–µ—Ä—Ç–∞–º (—Å–ø–µ—Ü–∏–∞–ª–∏—Å—Ç–∞–º –≤ –∏—Å—Å–ª–µ–¥—É–µ–º–æ–π –æ–±–ª–∞—Å—Ç–∏) –ø—Ä–µ–¥–ª–∞–≥–∞–µ—Ç—Å—è –ø—Ä–æ–≤–µ—Å—Ç–∏—Ä–∞–Ω–∂–∏—Ä–æ–≤–∞–Ω–∏–µ (—Ä–∞—Å–ø–æ–ª–æ–∂–µ–Ω–∏–µ —è–≤–ª–µ–Ω–∏–π –≤ –ø–æ—Ä—è–¥–∫–µ –≤–æ–∑—Ä–∞—Å—Ç–∞–Ω–∏—è (—É–±—ã–≤–∞–Ω–∏—è) –∑–Ω–∞—á–∏–º–æ—Å—Ç–∏) –Ω–µ–∫–æ—Ç–æ—Ä—ã—Ö —è–≤–ª–µ–Ω–∏–π (—Ü–µ–Ω–æ–æ–±—Ä–∞–∑—É—é—â–∏—Ö —Ñ–∞–∫—Ç–æ—Ä–æ–≤). –ü—Ä–∏ —ç—Ç–æ–º –∫–∞–∂–¥–æ–º—É —è–≤–ª–µ–Ω–∏—é (—Ñ–∞–∫—Ç–æ—Ä—É) –ø—Ä–∏—Å–≤–∞–∏–≤–∞–µ—Ç—Å—è —Å–≤–æ–π —Ä–∞–Ω–≥ (–ø–æ—Ä—è–¥–∫–æ–≤–æ–µ –º–µ—Å—Ç–æ—è–≤–ª–µ–Ω–∏—è (—Ñ–∞–∫—Ç–æ—Ä–∞) –≤ –æ–±—â–µ–π –ø–æ—Å–ª–µ–¥–æ–≤–∞—Ç–µ–ª—å–Ω–æ—Å—Ç–∏ —Ñ–∞–∫—Ç–æ—Ä–æ–≤). –Ý–∞–Ω–≥–∏ –ø—Ä–∏–Ω—è—Ç–æ –æ–±–æ–∑–Ω–∞—á–∞—Ç—å –ø–æ—Ä—è–¥–∫–æ–≤—ã–º–∏ —á–∏—Å–ª–∞–º–∏ –Ω–∞—Ç—É—Ä–∞–ª—å–Ω–æ–≥–æ —Ä—è–¥–∞ (1, 2, 3, 4 ......). –ü—Ä–∏ —ç—Ç–æ–º —Ä–∞–Ω–≥ 1 –ø—Ä–∏—Å–≤–∞–∏–≤–∞–µ—Ç—Å—è –Ω–∞–∏–±–æ–ª–µ–µ –∑–Ω–∞—á–∏–º–æ–º—É —Ñ–∞–∫—Ç–æ—Ä—É.
–°—É–º–º–∞ —Ä–∞–Ω–≥–æ–≤, –ø—Ä–æ—Å—Ç–∞–≤–ª–µ–Ω–Ω—ã—Ö —ç–∫—Å–ø–µ—Ä—Ç–æ–º –ø–æ –≤—Å–µ–º —Ñ–∞–∫—Ç–æ—Ä–∞–º –º–æ–∂–µ—Ç –±—ã—Ç—å –≤—ã—á–∏—Å–ª–µ–Ω–∞ –ø–æ —Å–ª–µ–¥—É—é—â–µ–π —Ñ–æ—Ä–º—É–ª–µ:
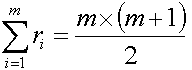
–≥–¥–µ
ri – ранг, поставленный i-ому фактору;
m – число исследуемых явления (факторов).
–°—É–º–º—ã —Ä–∞–Ω–≥–æ–≤ –ø—Ä–æ—Å—Ç–∞–≤–ª–µ–Ω–Ω—ã—Ö –∫–∞–∂–¥—ã–º —ç–∫—Å–ø–µ—Ä—Ç–æ–º –¥–æ–ª–∂–Ω—ã –±—ã—Ç—å —Ä–∞–≤–Ω—ã. –ï—Å–ª–∏ –∂–µ
—ç–∫—Å–ø–µ—Ä—Ç –ø—Ä–∏—Å–≤–∞–∏–≤–∞–µ—Ç –¥–≤—É–º (—Ç—Ä–µ–º –∏ —Ç–∞–∫ –¥–∞–ª–µ–µ) —Ä–∞–∑–ª–∏—á–Ω—ã–º —è–≤–ª–µ–Ω–∏—è–º –æ–¥–∏–Ω–∞–∫–æ–≤—ã–µ —Ä–∞–Ω–≥–∏, —Ç.–µ. —Å—á–∏—Ç–∞–µ—Ç –¥–≤–∞ —è–≤–ª–µ–Ω–∏—è (—Ñ–∞–∫—Ç–æ—Ä–∞) —Ä–∞–≤–Ω–æ–∑–Ω–∞—á–Ω—ã–º–∏ (—Å–≤—è–∑–∞–Ω–Ω—ã–µ —Ä–∞–Ω–≥–∏), —Ç–æ —Å—É–º–º—ã —Ä–∞–Ω–≥–æ–≤ –ø—Ä–æ—Å—Ç–∞–≤–ª–µ–Ω–Ω—ã–µ –∫–∞–∂–¥—ã–º —ç–∫—Å–ø–µ—Ä—Ç–æ–º –Ω–µ –±—É–¥—É—Ç —Å–æ–≤–ø–∞–¥–∞—Ç—å
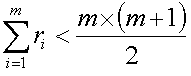
—á—Ç–æ –≤ —Å–≤–æ—é –æ—á–µ—Ä–µ–¥—å –Ω–µ –ø–æ–∑–≤–æ–ª–∏—Ç—å –ø—Ä–æ–∏–∑–≤–µ—Å—Ç–∏ –¥–∞–ª—å–Ω–µ–π—à–∏–µ —Ä–∞—Å—á–µ—Ç—ã.
–î–ª—è –∏–∑–±–µ–∂–∞–Ω–∏—è –Ω–∞—Ä—É—à–µ–Ω–∏—è –≤—ã—à–µ –ø—Ä–µ–¥—Å—Ç–∞–≤–ª–µ–Ω–Ω–æ–≥–æ —Ä–∞–≤–µ–Ω—Å—Ç–≤–∞, –æ—Ü–µ–Ω—â–∏–∫—É, –ø—Ä–æ–≤–æ–¥—è—â–µ–º—É —ç–∫—Å–ø–µ—Ä—Ç–∏–∑—É, –Ω–µ–æ–±—Ö–æ–¥–∏–º–æ –ø—Ä–æ–∏–∑–≤–µ—Å—Ç–∏ –ø–µ—Ä–µ—Å—á–µ—Ç —Ç–∞–∫–∏—Ö —Ä–∞–Ω–≥–æ–≤, –≤ —Ç–∞–∫ –Ω–∞–∑—ã–≤–∞–µ–º—ã–µ —Å—Ç–∞–Ω–¥–∞—Ä—Ç–∏–∑–∏—Ä–æ–≤–∞–Ω–Ω—ã–µ —Ä–∞–Ω–≥–∏. –Ý–∞—Å—á–µ—Ç –æ—Å—É—â–µ—Å—Ç–≤–ª—è–µ—Ç—Å—è –ø—É—Ç–µ–º –¥–µ–ª–µ–Ω–∏—è —Å—É–º–º—ã –º–µ—Å—Ç, –∑–∞–Ω–∏–º–∞–µ–º—ã—Ö —Å–≤—è–∑–∞–Ω–Ω—ã–º–∏ —Ä–∞–Ω–≥–∞–º–∏, –Ω–∞ –∏—Ö —á–∏—Å–ª–æ. –ü—Ä–∏–º–µ—Ä —Ä–∞—Å—á–µ—Ç–∞ –ø—Ä–µ–¥—Å—Ç–∞–≤–ª–µ–Ω –≤ —Ç–∞–±–ª–∏—Ü–µ 1.
‚Ññ —è–≤–ª–µ–Ω–∏—è (—Ñ–∞–∫—Ç–æ—Ä–∞) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | —Å—É–º–º–∞ |
–Ý–∞–Ω–≥, –ø—Ä–æ—Å—Ç–∞–≤–ª–µ–Ω–Ω—ã–π —ç–∫—Å–ø–µ—Ä—Ç–æ–º | 2 | 3 | 3 | 1 | 4 | 6 | 5 | 24 |
–Ý–∞–Ω–≥ —Ñ–∞–∫—Ç–æ—Ä–æ–≤ –ø–æ—Å–ª–µ –ø–µ—Ä–µ—Å—á–µ—Ç–∞ —Å–≤—è–∑–∞–Ω–Ω—ã—Ö —Ä–∞–Ω–≥–æ–≤ | 2 | 3,5 | 3,5 | 1 | 5 | 7 | 6 | 28 |
–í –∏—Ç–æ–≥–µ –º—ã –ø–æ–ª—É—á–∞–µ–º –Ω–æ—Ä–º–∞–ª—å–Ω—É—é —Ä–∞–Ω–∂–∏—Ä–æ–≤–∫—É, –¥–ª—è –∫–æ—Ç–æ—Ä–æ–π –≤—ã–ø–æ–ª–Ω–µ–Ω–æ –æ—Å–Ω–æ–≤–Ω–æ–µ —É—Å–ª–æ–≤–∏—è —Ä–∞–Ω–∂–∏—Ä–æ–≤–∞–Ω–∏—è (1).
–î–∞–ª–µ–µ –ø–æ –∫–∞–∂–¥–æ–º—É —è–≤–ª–µ–Ω–∏—é –ø–æ–¥—Å—á–∏—Ç—ã–≤–∞–µ—Ç—Å—è —Å—É–º–º–∞ —Ä–∞–Ω–≥–æ–≤, –ø—Ä–æ—Å—Ç–∞–≤–ª–µ–Ω–Ω—ã—Ö –∫–∞–∂–¥—ã–º —ç–∫—Å–ø–µ—Ä—Ç–∞–º. –Ø–≤–ª–µ–Ω–∏—é (—Ñ–∞–∫—Ç–æ—Ä—É), –∫–æ—Ç–æ—Ä—ã–π –ø–æ–ª—É—á–∏–ª –Ω–∞–∏–º–µ–Ω—å—à—É—é —Å—É–º–º—É —Ä–∞–Ω–≥–æ–≤, –ø—Ä–∏—Å–≤–∞–∏–≤–∞–µ—Ç—Å—è —Å–æ–æ—Ç–≤–µ—Ç—Å—Ç–≤–µ–Ω–Ω–æ–≥–æ —Ä–∞–Ω–≥ 1 –∏ —Ç.–¥. –ï—Å–ª–∏ –Ω–∞ –¥–∞–Ω–Ω–æ–º —ç—Ç–∞–ø–µ –¥–ª—è –Ω–µ–∫–æ—Ç–æ—Ä—ã—Ö —è–≤–ª–µ–Ω–∏—è —Å—É–º–º—ã —Ä–∞–Ω–≥–æ–≤ —Å–æ–≤–ø–∞–¥—É—Ç, —Ç–æ –Ω–µ–æ–±—Ö–æ–¥–∏–º–æ —Å–Ω–æ–≤–∞ –ø—Ä–æ–∏–∑–≤–µ—Å—Ç–∏ –ø—Ä–æ—Ü–µ–¥—É—Ä—É —Å—Ç–∞–Ω–¥–∞—Ä—Ç–∏–∑–∞—Ü–∏–∏ —Ä–∞–Ω–≥–æ–≤, –Ω–æ —É–∂–µ –ø–æ —Ä–∞–Ω–≥–∞–º, –ø–æ–ª—É—á–µ–Ω–Ω—ã–º –ø—É—Ç–µ–º —Å—É–º–º–∏—Ä–æ–≤–∞–Ω–∏—è –æ—Ü–µ–Ω–æ–∫ —ç–∫—Å–ø–µ—Ä—Ç–æ–≤. –ü—Ä–∏–º–µ—Ä —Ä–∞–Ω–∂–∏—Ä–æ–≤–∞–Ω–∏—è –ø—Ä–µ–¥—Å—Ç–∞–≤–ª–µ–Ω –≤ —Ç–∞–±–ª–∏—Ü–µ 2. –ù–µ–æ–±—Ö–æ–¥–∏–º–æ –æ—Ç–º–µ—Ç–∏—Ç—å, —á—Ç–æ —á–∏—Å–ª–æ —ç–∫—Å–ø–µ—Ä—Ç–æ–≤ (d) –¥–æ–ª–∂–Ω–æ –±—ã—Ç—å –∫–∞–∫ –º–∏–Ω–∏–º—É–º –Ω–∞ 1 –±–æ–ª—å—à–µ, —á–µ–º —á–∏—Å–ª–æ –∏—Å—Å–ª–µ–¥—É–µ–º—ã—Ö —Ñ–∞–∫—Ç–æ—Ä–æ–≤ (m).
–§–∞–∫—Ç–æ—Ä—ã |
–≠–∫—Å–ø–µ—Ä—Ç | 1 | 2 | 3 | 4 | 5 | 6 | | —Å—É–º–º–∞ |
1 | 2 | 3 | 3 | 1 | 4 | 6 | 5 | 24 |
2 | 1 | 3 | 4 | 2 | 4 | 5 | 6 | 25 |
3 | 1 | 2 | 4 | 3 | 5 | 6 | 7 | 28 |
4 | 2 | 4 | 3 | 1 | 5 | 7 | 6 | 28 |
5 | 1 | 3 | 4 | 2 | 4 | 6 | 5 | 25 |
6 | 2 | 3 | 4 | 1 | 5 | 6 | 7 | 28 |
7 | 1 | 3 | 4 | 2 | 5 | 6 | 7 | 28 |
8 | 3 | 2 | 4 | 1 | 5 | 7 | 6 | 28 |
–°—Ç–∞–Ω–¥–∞—Ä—Ç–∏–∑–∏—Ä–æ–≤–∞–Ω–Ω—ã–µ —Ä–∞–Ω–≥–∏ |
1 | 2 | 3,5 | 3,5 | 1 | 5 | 7 | 6 | 28 |
2 | 1 | 3 | 4,5 | 2 | 4,5 | 6 | 7 | 28 |
3 | 1 | 2 | 4 | 3 | 5 | 6 | 7 | 28 |
4 | 2 | 4 | 3 | 1 | 5 | 7 | 6 | 28 |
5 | 1 | 3 | 4,5 | 2 | 4,5 | 7 | 6 | 28 |
6 | 2 | 3 | 4 | 1 | 5 | 6 | 7 | 28 |
7 | 1 | 3 | 4 | 2 | 5 | 6 | 7 | 28 |
8 | 3 | 2 | 4 | 1 | 5 | 7 | 6 | 28 |
–°—É–º–º–∞ —Ä–∞–Ω–≥–æ–≤ (r1) | 13 | 23,5 | 31,5 | 13 | 39 | 52 | 52 | |
–Ý–∞–Ω–≥–∏ —Ñ–∞–∫—Ç–æ—Ä–æ–≤ (R) | 1 | 2 | 3 | 1 | 4 | 5 | 5 | 21 |
–°—Ç–∞–Ω–¥–∞—Ä—Ç–∏–∑–∏—Ä–æ–≤–∞–Ω–Ω—ã–µ –∏—Ç–æ–≥–æ–≤—ã–µ —Ä–∞–Ω–≥–∏ | 1,5 | 3 | 4 | 1,5 | 5 | 6,5 | 6,5 | 28 |
–ü–æ–ª—É—á–µ–Ω–∏–µ —Ä–∞–Ω–≥–æ–≤ –ø–æ–∑–≤–æ–ª—è–µ—Ç –ø—Ä–æ–∏–∑–≤–µ—Å—Ç–∏ –¥–∞–ª—å–Ω–µ–π—à–∏–µ —Ä–∞—Å—á–µ—Ç—ã –≤–µ—Å–æ–≤—ã—Ö –∫–æ—ç—Ñ—Ñ–∏—Ü–∏–µ–Ω—Ç–æ–≤ –¥–ª—è –∫–∞–∂–¥–æ–≥–æ —Ü–µ–Ω–æ–æ–±—Ä–∞–∑—É—é—â–µ–≥–æ —Ñ–∞–∫—Ç–æ—Ä–∞ –ø—Ä–∏ –ø—Ä–æ–≤–µ–¥–µ–Ω–∏–∏ –∫–æ—Ä—Ä–µ–∫—Ç–∏—Ä–æ–≤–æ–∫ –≤ –∫–≤–∞–ª–∏–º–µ—Ç—Ä–∏—á–µ—Å–∫–∏—Ö –º–æ–¥–µ–ª—è—Ö –∏ –¥—Ä—É–≥–∏—Ö –º–µ—Ç–æ–¥–∞—Ö —Å—Ä–∞–≤–Ω–∏—Ç–µ–ª—å–Ω–æ–≥–æ –ø–æ–¥—Ö–æ–¥–∞. –û–¥–Ω–∞–∫–æ –æ–∫–æ–Ω—á–∞—Ç–µ–ª—å–Ω—ã–π –≤—ã–≤–æ–¥ –æ –≤–æ–∑–º–æ–∂–Ω–æ—Å—Ç–∏ –∏—Å–ø–æ–ª—å–∑–æ–≤–∞–Ω–∏—è –∫–æ–ª–ª–µ–∫—Ç–∏–≤–Ω–æ–≥–æ –º–Ω–µ–Ω–∏—è —ç–∫—Å–ø–µ—Ä—Ç–æ–≤ –≤–æ–∑–º–æ–∂–Ω–æ –ø–æ—Å–ª–µ –æ–ø—Ä–µ–¥–µ–ª–µ–Ω–∏—è —Å–æ–≥–ª–∞—Å–æ–≤–∞–Ω–Ω–æ—Å—Ç–∏ –º–Ω–µ–Ω–∏–π —ç–∫—Å–ø–µ—Ä—Ç–æ–≤. –ü—Ä–æ–≤–µ—Ä–∫—É —Å–æ–≥–ª–∞—Å–æ–≤–∞–Ω–Ω–æ—Å—Ç–∏ –º–Ω–µ–Ω–∏–π –æ—Å—É—â–µ—Å—Ç–≤–ª—è—é—Ç —Å –ø–æ–º–æ—â—å—é –∫–æ—ç—Ñ—Ñ–∏—Ü–∏–µ–Ω—Ç–∞ –∫–æ–Ω–∫–æ—Ä–¥–∞—Ü–∏–∏ (—Å–æ–≥–ª–∞—Å–∏—è). –Ý–∞—Å—á–µ—Ç –∫–æ—ç—Ñ—Ñ–∏—Ü–∏–µ–Ω—Ç–∞ –æ—Å—É—â–µ—Å—Ç–≤–ª—è–µ—Ç –ø–æ —Å–ª–µ–¥—É—é—â–µ–π —Ñ–æ—Ä–º—É–ª–µ:
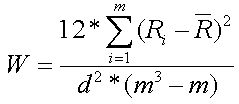
–≥–¥–µ,
m – количество оцениваемых факторов;
d – число экспертов;
Ri – сумма рангов по i-ому фактору (явлению);
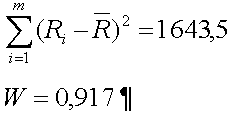
–ß–µ–º –±–ª–∏–∂–µ –∑–Ω–∞—á–µ–Ω–∏–µ –∫–æ—ç—Ñ—Ñ–∏—Ü–∏–µ–Ω—Ç–∞ –∫ 1, —Ç–µ–º –≤—ã—à–µ —Å–æ–≥–ª–∞—Å–æ–≤–∞–Ω–Ω–æ—Å—Ç—å. –ü—Ä–∏–µ–º–ª–µ–º–æ—Å—Ç—å –ø–æ–ª—É—á–µ–Ω–Ω—ã—Ö —ç–∫—Å–ø–µ—Ä—Ç–Ω—ã—Ö –æ—Ü–µ–Ω–æ–∫ –æ–ø—Ä–µ–¥–µ–ª—è–µ—Ç—Å—è –ø—É—Ç–µ–º —Å—Ä–∞–≤–Ω–µ–Ω–∏—è –∫—Ä–∏—Ç–µ—Ä–∏—è –∑–Ω–∞—á–∏–º–æ—Å—Ç–∏ x2—Ñ–∞–∫—Ç=d*(m-1)*W —Å —Ç–∞–±–ª–∏—á–Ω—ã–º –∑–Ω–∞—á–µ–Ω–∏–µ–º x —Ç–∞–±–ª. –ø—Ä–∏ —Å—Ç–µ–ø–µ–Ω—è—Ö —Å–≤–æ–±–æ–¥—ã (m-1) –∏ –∑–∞–¥–∞–Ω–Ω–æ–π –≤–µ—Ä–æ—è—Ç–Ω–æ—Å—Ç—å—é (–Ω–∞–ø—Ä–∏–º–µ—Ä: P–æ = 0,05, P=1-Po). –ï—Å–ª–∏ –ø–æ–ª—É—á–µ–Ω–Ω–æ–µ —Ä–∞—Å—á–µ—Ç–Ω—ã–º –ø—É—Ç–µ–º –∑–Ω–∞—á–µ–Ω–∏–µ —Ä–∞–≤–Ω–æ –∏–ª–∏ –≤—ã—à–µ —Ç–∞–±–ª–∏—á–Ω–æ–≥–æ, —Ç–æ –∫–æ—ç—Ñ—Ñ–∏—Ü–∏–µ–Ω—Ç –∫–æ–Ω–∫–æ—Ä–¥–∞—Ü–∏–∏ —Å—É—â–µ—Å—Ç–≤–µ–Ω–µ–Ω –∏ —Å –Ω–∞–¥–µ–∂–Ω–æ—Å—Ç—å—é 0,95, –º–Ω–µ–Ω–∏—è —ç–∫—Å–ø–µ—Ä—Ç–æ–≤ —Å–æ–≥–ª–∞—Å–æ–≤–∞–Ω–Ω—ã. –¢–∞–±–ª–∏—á–Ω—ã–µ –∑–Ω–∞—á–µ–Ω–∏—è –∫—Ä–∏—Ç–µ—Ä–∏—è –∑–Ω–∞—á–∏–º–æ—Å—Ç–∏ –ø—Ä–µ–¥—Å—Ç–∞–≤–ª–µ–Ω—ã –≤ —Ç–∞–±–ª–∏—Ü–µ 3.
m-1 | P0 | | m-2 | P0 |
0,05 | 0,01 | 0 | 0,05 | 1 | 0 |
1 | 3,84 | 6,63 | 10,83 | 16 | 26,3 | 32 | 39,25 |
2 | 5,99 | 9,21 | 13,81 | 17 | 27,59 | 33,41 | 40,79 |
3 | 7,81 | 1134 | 16,27 | 18 | 28,87 | 34,8 | 42,31 |
4 | 9,49 | 13,28 | 18,46 | 19 | 30,14 | 36,19 | 43,82 |
5 | 11,07 | 15,09 | 20,52 | 20 | 31,41 | 37,57 | 45,31 |
6 | 12,59 | 16,81 | 22,46 | 21 | 32,67 | 38,93 | 46,8 |
7 | 14,07 | 18,47 | 24,32 | 22 | 33,92 | 40,29 | 48,27 |
8 | 15,51 | 20,09 | 26,12 | 23 | 35,17 | 41,63 | 49,73 |
9 | 16,92 | 21,67 | 27,88 | 24 | 36,41 | 42,98 | 51,18 |
10 | 18,31 | 23,21 | 29,59 | 25 | 37,65 | 44,31 | 52,62 |
11 | 19,67 | 24,72 | 31,26 | 26 | 38,88 | 45,64 | 54,05 |
12 | 21,03 | 26,22 | 32,91 | 27 | 40,11 | 46,96 | 55,48 |
13 | 22,37 | 27,69 | 34,53 | 28 | 41,34 | 48,28 | 56,89 |
14 | 23,68 | 29,14 | 36,12 | 29 | 42,56 | 49,59 | 58,3 |
15 | 25 | 30,58 | 37,7 | 30 | 43,77 | 50,89 | 59,7 |
x2—Ñ–∞–∫—Ç= 44,016 > x2—Ç–∞–±–ª.= 12,59
–¢–∞–∫–∏–º –æ–±—Ä–∞–∑–æ–º, –º–Ω–µ–Ω–∏—è —ç–∫—Å–ø–µ—Ä—Ç–æ–≤, –ø—Ä–∏–≤–µ–¥–µ–Ω–Ω—ã–µ –≤ –Ω–∞—à–µ–º –ø—Ä–∏–º–µ—Ä–µ, –¥–æ—Å—Ç–∞—Ç–æ—á–Ω–æ —Å–æ–≥–ª–∞—Å–æ–≤–∞–Ω–Ω—ã –∏ –º–æ–≥—É—Ç –±—ã—Ç—å –∏—Å–ø–æ–ª—å–∑–æ–≤–∞–Ω—ã –≤ –¥–∞–ª—å–Ω–µ–π—à–∏—Ö —Ä–∞—Å—á–µ—Ç–∞—Ö.
–í–µ—Å–æ–≤–æ–π –∫–æ—ç—Ñ—Ñ–∏—Ü–∏–µ–Ω—Ç –∫–∞–∂–¥–æ–º—É —Ñ–∞–∫—Ç–æ—Ä—É –º–æ–∂–µ—Ç –±—ã—Ç—å –ø—Ä–∏—Å–≤–æ–µ–Ω —Å –ø–æ–º–æ—â—å—é —Å–ª–µ–¥—É—é—â–µ–π —Ñ–æ—Ä–º—É–ª—ã:
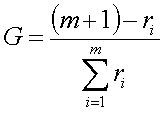
ri – итоговый ранг фактора.
–í –Ω–∞—à–µ–º –ø—Ä–∏–º–µ—Ä–µ –≤–µ—Å–∞ —Ä–∞—Å–ø—Ä–µ–¥–µ–ª–∏–ª–∏—Å—å –±—ã —Å–ª–µ–¥—É—é—â–∏–º –æ–±—Ä–∞–∑–æ–º (—Ç–∞–±–ª–∏—Ü–∞ 4).
–§–∞–∫—Ç–æ—Ä—ã |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | —Å—É–º–º–∞ |
–Ý–∞–Ω–≥ | 1,5 | 3 | 4 | 1,5 | 5 | 6,5 | 6,5 | 24 |
–í–µ—Å | 0,23 | 0,18 | 0,14 | 0,23 | 0,11 | 0,05 | 0,05 | 1 |
Представленный способ распределения весов не претендует на объективность, и обладает рядом недостатков, в частности: распределение весов основано на ранжирование факторов, что в свою очередь позволяет распределить факторы только с заданным интервалом, т.е. метод дает ответ, что фактор «А» важнее чем «Б», а «Б» важнее чем «С». Однако, согласно этому фактор «А» в два раза важнее чем фактор «С», что может не соответствовать действительности.
–°–æ—Ç–Ω–∏–∫–æ–≤ –Ý–æ–º–∞–Ω,
–Ω–∞—á–∞–ª—å–Ω–∏–∫ –æ—Ç–¥–µ–ª–∞ –æ—Ü–µ–Ω–∫–∏